Andrzej Więckowski, Ph.D.

$\alpha$-shapes

In this blog post, I want to show you an effective method for mesh reconstruction from point clouds. No edge constraints are needed! No opaque AI black box—just an analytically controlled, user-defined solution. Let me introduce you to $\alpha$-shapes [1].

What is an $\alpha$-shape?

$\alpha$-shapes are a generalization of the convex hull used in computational geometry to describe the “shape” of a set of points. Every convex hull is an $\alpha$-shape, but not every $\alpha$-shape is a convex hull. By adjusting the parameter $\alpha$, you can control the level of detail in the shape: larger values allow more concavity, while smaller values smooth the shape toward the convex hull (cf. Figure 1). This parameter also influences the formation of holes in the shape.

In this post, I’ll focus on $\alpha$-shapes derived from Delaunay triangulation. The algorithm for computing an $\alpha$-shape from a collection of points is relatively straightforward. First, perform a Delaunay triangulation. Then, apply a filter to remove any triangle whose circumradius satisfies the condition $R^2 > \alpha^{-1}$. Algorithm 1 shows a pseudocode version of the $\alpha$-shape filter. Keep in mind that a proper implementation is significantly more complex. You can visit BurstTriangulator package, which I authored, to see a complete example. Note that this straightforward implementation is somewhat brute-force, in many applications, additional constraints on triangle removal should be considered. If $\alpha = 0$, then you immediately obtain the convex hull—no triangle is removed!

Why does this work? Essentially, Delaunay triangulation produces a triangle mesh that covers the convex hull of the input points. Boundary triangles in this hull tend to have large circumradii ($R$), making them prime candidates for removal by the $\alpha$-shape filter. By adjusting the $\alpha$ value, you control the size of features that are retained or removed. Figure 2 illustrates an example of the algorithm: on the left, a triangulated collection of points; on the right, the resulting mesh after applying the $\alpha$-shape filter.

Why not use triangle area instead? The circumradius directly measures how “spread out” a triangle is. A small circumradius means the triangle tightly encloses its vertices, which is desirable when identifying meaningful geometric features. In contrast, triangle area can be misleading—it may be large for compact triangles (like equilateral ones) and small for long, thin triangles. Therefore, area is not a reliable indicator of geometric tightness. Using circumradius ensures the algorithm respects the geometry and topology implied by Delaunay triangulation, whereas area does not capture this structure effectively.

Applications

One of the most common applications of $\alpha$-shapes is mesh reconstruction from point clouds. In this process, the user doesn’t need to define complex constraints—mesh generation, including hole support, is controlled by a single parameter: $\alpha$. In Figure 3, you can see an animation where points are first triangulated, then the $\alpha$-shape filter is applied for various values of $\alpha$, progressively removing triangles. While this method isn’t perfect, I believe the reconstruction of the letter “A” is a notable result! The rules for triangle removal can also be easily customized to produce better or more interesting results, depending on the application.

Another compelling application of $\alpha$-shapes is procedural mesh generation. These meshes can be used in virtual environments—for example, as maps in RTS games or other genres that require dynamic world maps. Figure 4 shows an animation of procedurally generated meshes using the $\alpha$-shape filter. The process begins with generating random points within the unit square, followed by Delaunay triangulation. Finally, the $\alpha$-shape filter is applied, along with additional settings to ensure a continuous, 1-colorable mesh.

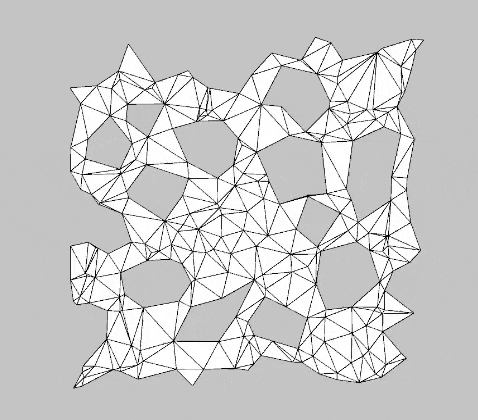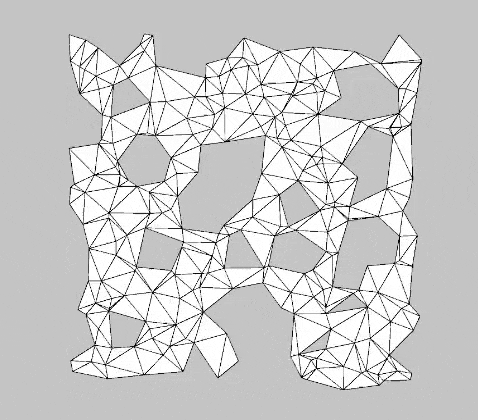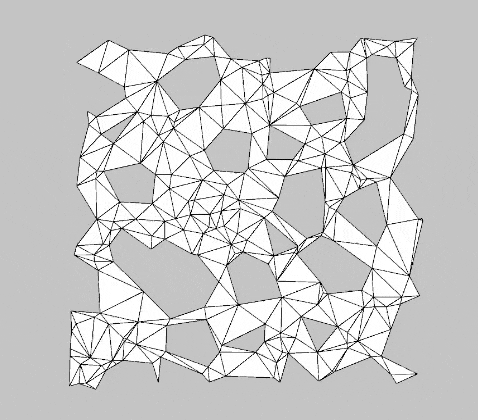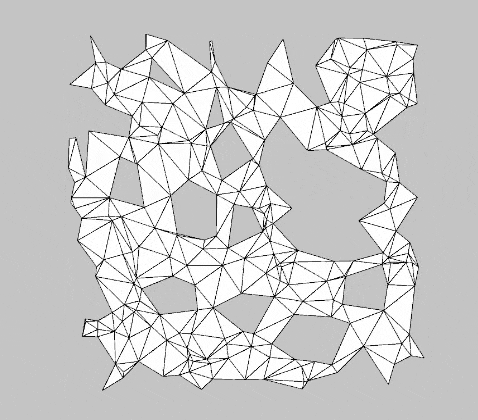
With the BurstTriangulator package, generating examples like the one in Figure 4 is straightforward. Below is a minimal working example to show how it can be done. Keep in mind that this implementation can be further optimized using Unity.Burst and, more importantly, extensively customized for various use cases.

var random = new Unity.Mathematics.Random(seed: 42);
var managedPositions = Enumerable.Range(0, 128).Select(_ => random.NextDouble2()).ToArray();
using var positions = new NativeArray(managedPositions, Allocator.Persistent);
using var triangulator = new Triangulator(Allocator.Persistent)
{
    Input = { Positions = positions },
    Settings = {
      UseAlphaShapeFilter = true,
      AlphaShapeSettings =
      {
          Alpha = 500,
          PreventWindmills = true, // Important for obtaining continous mesh!
          ProtectPoints = true,
      },
    },
};

triangulator.Run();

References

1. H. Edelsbrunner, D. Kirkpatrick, R. Seidel. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory, 29(4): 551–559 (1983). ↩
2. Alpha shape. Wikipedia. Retrieved April 25, 2025. Figure authored by Sigbert, CC BY-SA 3.0, via Wikimedia Commons. ↩

[Top]