Andrzej Więckowski, Ph.D. — personal webpage

Rodrigues’ formula

In this post, I will introduce you to a great tool: Rodrigues’ formula. This is not the Rodrigues associated with Tarantino’s films, but you’ll soon see that he is just as brilliant. Let’s dive in!

I often encounter geometric problems in the projects I work on. Since these projects require runtime solutions, I perform analytical derivations and calculations on paper for optimization purposes. Many people struggle when dealing with rotation-related problems. In this post, I would like to present a very powerful tool: the operator representation of Rodrigues’ rotation formula. This formula enables elegant analytical proofs for rotation-related problems without the need to work with quaternions or matrices. If you’re a physicist, I believe you’ll particularly appreciate this approach and might even wonder, why wasn’t this covered in my studies?!

Rodrigues’ formula for a rotation $R$ by an angle $\theta$ around a direction $u$ is given by

$$ R = R_u(\theta) = \cos \theta \,\,\mathbb 1 + \sin\theta \,\,[u]_\times + (1- \cos \theta) \,\,u \otimes u\,, $$

where $[u]_{\times}$ is the cross matrix defined as $$ [u]_\times v = u \times v\,, $$ and $u \otimes u$ is the Kronecker product (outer product): $$ u \otimes u = u u ^\mathsf{T}. $$ As you can see, this form of rotation is composed solely of abstract operators, which can be used for analytical proofs. Applying this operator to any vector $v$ gives

$$ R\,\,v = \cos \theta \,\,v + \sin\theta \,\,u\times v+ (1- \cos \theta)(u\cdot v)\,\, u\,. $$

Similarly, we can construct a quaternion representation of the rotation $q$ using Euler’s formulas $$ q = (\cos \tfrac\theta2, u\sin \tfrac \theta2). $$ Personally, I prefer Rodrigues’ operator representation, as it seems more human-friendly.

meme — Rodrigues’ formula is an elegant and convenient tool for handling rotations.

Example

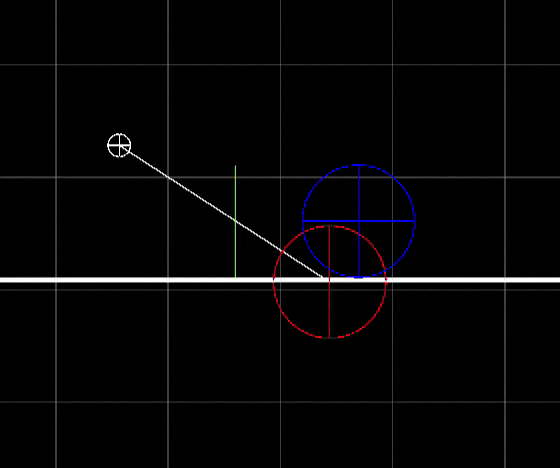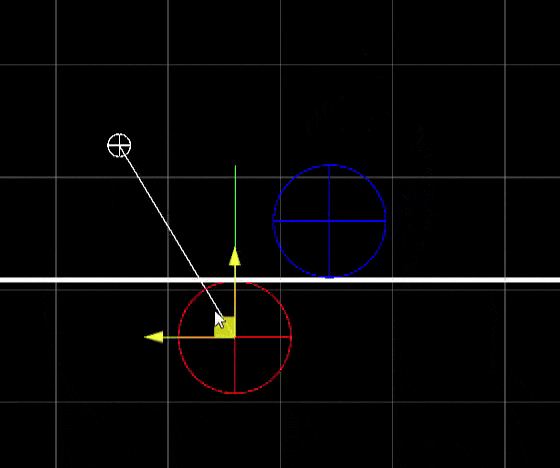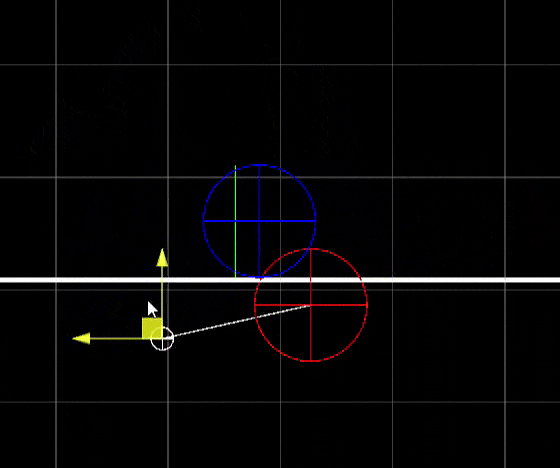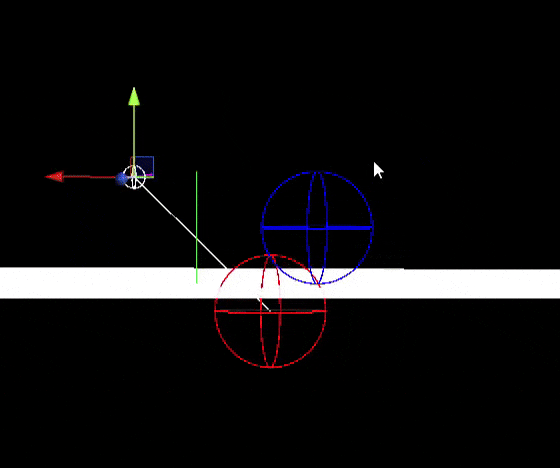
Consider a sphere of radius $r$ at point $A$, a plane defined by point $B$ and normal direction $n$, and a pivot rotation at point $P$ along direction $u$ (see Figure 2). Find the rotation $R_u(\theta)$ with the smallest absolute value of $\theta$ such that the sphere no longer collides with the plane and remains above it.

Based on the problem constraints, we can construct the following system of equations: $$ \begin{cases} \| A' - A'' \| = r\,, \\[1ex] A' = R(A-P) + P\,, \\[1ex] A'' = A' - [(A' - B)\cdot n] \, n\,, \\[1ex] (A' - A'')\cdot n > 0\,,\\[1ex] \theta \to \displaystyle\min_{\|\theta\|} R_u(\theta)\,, \end{cases} $$ where $A'$ is $A$ after the application of rotation $R$, and $A''$ is $A'$ projected onto the plane defined by $B$ and $n$. From the first equation, we get $$ \| A' \|^2 + \|A''\|^2 - 2 A'\cdot A'' = r^2\,.$$ Using the third equation, we can express $|A''|^2$ and $A'\cdot A''$:

$$ \|A''\|^2 = \|A'\|^2 + [(A'-B)\cdot n]^2 - 2 (A'-B)\cdot n \,(A' \cdot n)\,,$$

$$ A'\cdot A'' = A' \cdot \left(A' - [(A' - B)\cdot n] \, n\right) = \|A'\|^2 - (A'-B)\cdot n \,(A' \cdot n)\,.$$

Returning to the first equation, we obtain

$$ \begin{align} r^2 &= \| A' \|^2 + \|A''\|^2 - 2 A'\cdot A'' =\\ &= \| A' \|^2 + \|A'\|^2 + [(A'-B)\cdot n]^2 - 2 (A'-B)\cdot n \,(A' \cdot n) - 2\|A'\|^2 + 2 (A'-B)\cdot n \,(A' \cdot n)=\\ &= [(A'-B)\cdot n]^2 = [(R(A-P)+P-B)\cdot n]^2\,. \end{align} $$

The final equation simplifies significantly $$ [(R(A-P)+P-B)\cdot n]^2 = r^2\,. $$ Taking the square root of both sides (carefully keeping the $\pm$ to avoid losing solutions): $$ [R(A-P)+P-B]\cdot n = \pm r\,, $$ $$ n R(A-P)= n\cdot(B-P)\pm r\,. $$ Substituting Rodrigues’ formula leads to a trigonometric equation $$ a\cos\theta + b \sin\theta = c_\pm\,, $$ where $$ \begin{cases} a = n\cdot(A-P)-(n\cdot u) \, [u \cdot(A-P)]\,,\\[1ex] b = n\cdot[u\times(A-P)]\,,\\[1ex] c_\pm = n\cdot(B-P) - (n\cdot u)\, [u\cdot(A-P)] \pm r\,.\\ \end{cases} $$ This equation can be solved by substituting $\cos \theta = x$, however, I used symbolic computation (via WolframAlpha) to obtain the solution: $$\begin{align} \theta_{0,\pm} = 2 \,\texttt{atan2}(b + \sqrt{\Delta_\pm}, a + c_\pm)\,, \\[1ex] \theta_{1,\pm} = 2 \,\texttt{atan2}(b - \sqrt{\Delta_\pm}, a + c_\pm)\,, \end{align} $$ where $$ \Delta_\pm = a ^2 + b ^2 - c_\pm ^2\,.$$ Note: The equation may have 0, 1, 2, (3?), or 4 valid solutions It would be interesting to plot the number of solutions in phase space. (in $\mathbb R$). We are interested in the solution with the smallest absolute value that aligns with the normal direction of the plane $n$. The condition $(A'-A'')\cdot n > 0$ can be reduced to: $$ (A'-B)\cdot n >0\,. $$ Before solving the equation, it is useful to check a “quick exit” condition. If the sphere-plane distance is greater than the radius $r$ and the sphere is above the plane, the condition is already satisfied. This can be expressed as follows: $$ \|(A-B)\cdot n\| \ge r \,\,\wedge\,\, (A-B)\cdot n > 0\,. $$ Below is an example implementation with Unity.Burst support and a visualization using gizmos (see Figure 3).

The solution preview animation. The red sphere represents $A$, the blue sphere represents $A'$, the white point is $P$, the green arrow indicates $n$, and the magenta arrow represents $u$.

public static bool Solve(float3 A, float r, float3 B, float3 P, float3 u, float3 n, out float theta)
  {
      static float delta(float a, float b, float c) => a * a + b * b - c * c;
      static float clip(float angle) => angle > math.PI ? angle - 2 * math.PI : angle < -math.PI ? angle + 2 * math.PI : angle;
      static float2 quadratic(float a, float b, float c, float delta) => 2 * math.atan2(math.float2(b + math.sqrt(delta), b - math.sqrt(delta)), a + c);
      float3 Aprim(float theta) => math.cos(theta) * (A - P) + math.sin(theta) * math.cross(u, A - P) + (1 - math.cos(theta)) * u * math.dot(u, A - P) + P;
      bool accept(float theta, float minThetaAbs) => math.abs(theta) < minThetaAbs && math.dot(Aprim(theta) - B, n) > 0;

      (float theta, float thetaAbs) trysolve(float a, float b, float c, float theta, float minThetaAbs)
      {
          var d = delta(a, b, c);
          if (d >= 0)
          {
              var thetas = quadratic(a, b, c, d);
              var theta0 = clip(thetas[0]);
              var theta1 = clip(thetas[1]);
              (theta, minThetaAbs) = accept(theta0, minThetaAbs) ? (theta0, math.abs(theta0)) : (theta, minThetaAbs);
              (theta, minThetaAbs) = accept(theta1, minThetaAbs) ? (theta1, math.abs(theta1)) : (theta, minThetaAbs);
          }
          return (theta, minThetaAbs);
      }

      // Quick exit: if collision sphere does not collide with plane and its above of it.
      var abn = math.dot(A - B, n);
      if (math.abs(abn) >= r && abn > 0)
      {
          theta = default;
          return false;
      }

      var a = math.dot(n, A - P) - math.dot(n, u) * math.dot(u, A - P);
      var b = math.dot(n, math.cross(u, A - P));
      var c = math.dot(n, B - P) - math.dot(n, u) * math.dot(u, A - P);

      theta = float.NaN;
      var minThetaAbs = float.MaxValue;
      (theta, minThetaAbs) = trysolve(a, b, c + r, theta, minThetaAbs);
      (theta, minThetaAbs) = trysolve(a, b, c - r, theta, minThetaAbs);

      return !math.isnan(theta);
  }

[Top]